Assessing Process Performance Using Cpk and Cp
To determine how a process is operating, we can calculate:
- Process Capability Index (Cpk).
- Process Capability (Cp).
Calculating Cpk
Cpk are classified into two; the upper and the lower denoted Cpu and CpL respectively.
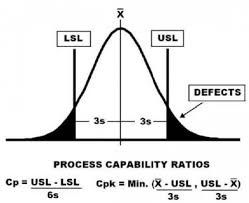
We are dividing by 3 because specification limit has an upper bound and a lower bound and since 6 sigmas (i.e. 6 standard deviations) account for nearly all eventualities on a process (assuming normal distribution), hence dividing by 3 enables us to look at only one side of the distribution.
Calculating Cpk using a Z Value
Cpk can be determined by dividing the Z score by 3.Z = x – mean of the population / standard deviation.
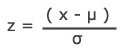
Interpretation of Cpk & Centered Processes
- If a process is perfectly centered, it has a Cp of 1 indicating that the mean was 3 standard deviations (sigma) away from the upper limit and the lower limit.
- And, a perfectly centered process a process who has a mean exactly in between the 2 specification limits will have a Cpk of 1.
Deductions from the Values of Cpk
- Cpk measures how close a process is performing compared to its specification limits and accounting for the inherent process variability.
- The larger the Cpk value, the less likely the item will be outside the specification limits.
- When Cpk is negative, the process under study will produce output that is outside the customer specification limits.
- Cpk is negative when the mean of the process is outside the customer specification limits.
- At least Cpk = 1.33 [4 sigma] or higher is required to satisfy most customers.
- Cpk do have upper and lower value reported. If the upper value is 2 and the lower is 1, we say it has been shifted to the left.
Cpk Values
Cpk = Negative number, process is out of customer’s specification.
Cpk = 0.5, good chance of process meeting customer’s specification.
Cpk = 1, process about meeting customer’s specification.
Cpk = 2, Great! Process meets customer’s specification but can be improved upon.
Cpk =3, Excellent result.
Calculating Cp
Cp does not account for centering.
Cp = (USL – LSL) / ( 6 x σr )
Cp = (USL – LSL) / (6 x R Bar / d2)
Cp for Process Mean close to USL
If Process Mean (I.e. central tendency) is closer to the USL, use:
[USL – X (bar) ] / [3 x R Bar / d2], where X (bar) is the Process Mean.
Cp for Process Mean close to LSL
If Process mean (i.e. central tendency) is closer to the LSL, use:
[x(bar) – LSL ] / [3 x R Bar / d2], where x(bar) is the Process Mean.
Capability Ratio Cr
The inverse of Cp equals the Capability Ratio (Cr)
Cr = 1/ Cp = ( 6 x σr ) / (USL – LSL)
If Cr < 0.75, the process is capable
If Cr = 0.75 – 1.00, the process is capable with tight control.
If Cr >1, the process is not capable.
Conclusion on Cp & Cpk
- If Cp == Cpk, then the process is perfectly centered and, if process is perfectly centered, Cp == Cpk.
- Cpk can never be larger than Cp, because Cpk accounts for centering (while Cp does not),
- Both processes are assumed stable.
About the Author
Adebayo is a thought leader in continuous process improvement and manufacturing excellence. He is a Certified Six Sigma Master Black Belt (CSSMBB) Professional and Management Systems Lead Auditor (ISO 9001, 45001, ISO 22000/FSSC 22000 etc.) with strong experience leading various continuous improvement initiative in top manufacturing organizations.
You can reach him here.
